Elli Anastasiadi

Modeling and Verification

This course is currently offered at the PhD level with the purpose of becoming a bachelor level course in the future. It corresponds to 7ECTS.

Prerequisites

This course does not have any need for previously taken courses; it is self-contained. The following topics are related to the contents:

• Automata Theory
• Mathematical Logic
• Discrete Mathematics
• Complexity Theory
• Algorithms and Data Structures

The course book (see below) will contain a summary of the issues in these areas that are relevant to this course. We believe that this course is also well-suited for students in electrical engineeering and mathematics.

Materials

The course will basically cover Chapters 1 through 7.

Additional literature:

• E.M. Clarke, O. Grumberg, D.A. Peled: Model Checking, MIT Press, 1999

• M. Huth and M.D. Ryan: Logic in Computer Science – Modelling and Reasoning about Systems, Cambridge University Press, 2nd edition, 2004

• K. Schneider: Verification of Reactive Systems, Springer-Verlag, Texts in Theoretical Computer Science. An EATCS Series, 2004

Contents of the Course

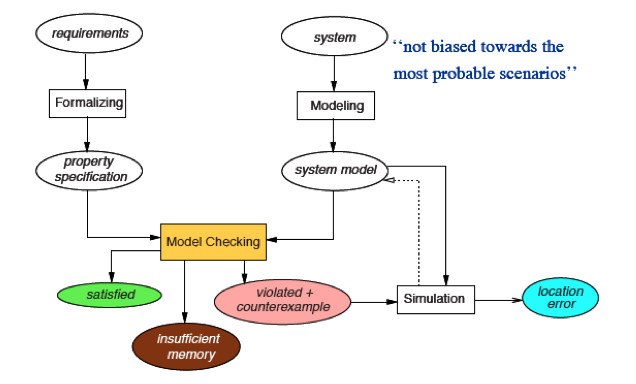
In this course we will focus on the theory and practice of model checking: the primary formal verifiation teqnique that is currently in use.

Model checking is based on checking models. So, we first start by explaining what models are, and will make clear that so-called labeled transition systems, a model that is akin to automata, are suitable for modeling sequential, as well as multi-threading programs.

This is followed by a detailed study on various classes of system properties such as safety, liveness, and fairness. It will be shown how finite automata as well as variants thereof that accept infinite words are suitable for verifying regular properties.

The linear-time and branching time temporal logics LTL and CTL are then introduced and compared. Model checking algorithms for these logics together with detailed complexity considerations are covered.

Finally, abstraction techniques based on bisimulation and simulation relations are covered. These techniques are at key techniques to combat the state explosion problem.

Further motivation

The topics we will cover in this course have been consistently recognised as some of the most important and infuential works withing computer science.

In 1996, the ACM awarded the prestigious Turing Award – the Nobel Prize in Computer Science – to Amir Pnueli, for establishing Temporal Logic as a tool within formal methods. Later, in 2008, the pioneers of Model Checking: Ed Clarke, Allen Emerson, and Joseph Sifakis were awarded the same prize. The work of Leslie Lamport was also heavily influential in these fields and landed him the same honour in 2013.

Why?
Because their work led to the huge evolution of model checking in the last twenty-five years into a widely used verification and debugging technique for both software and hardware.

It is used (and further developed) by companies and institutes such as IBM, Intel, NASA, Cadence, Microsoft, and Siemens, to mention a few, and has culminated in a series of mostly freely downloadable software tools that allow the automated verification of, for instance, C#-programs or combinational hardware circuits.

Subtle errors, for instance due to multi-threading, that remain undiscovered using simulation or peer reviewing can potentially be revealed using model checking.  Model checking is thus an effective technique to expose potential design errors and improve software and hardware reliability.

But how does it work, that is, what are its underlying principles?
That’s exactly the focus of this lecture series!

We will show that model checking is based on well-known paradigms from automata theory, graph algorithms, logic, and data structures. Its complexity is analyzed using standard techniques from complexity theory.